[백준] 11051번 - 이항 계수 2 [Java]

문제 링크

---

문제 풀이

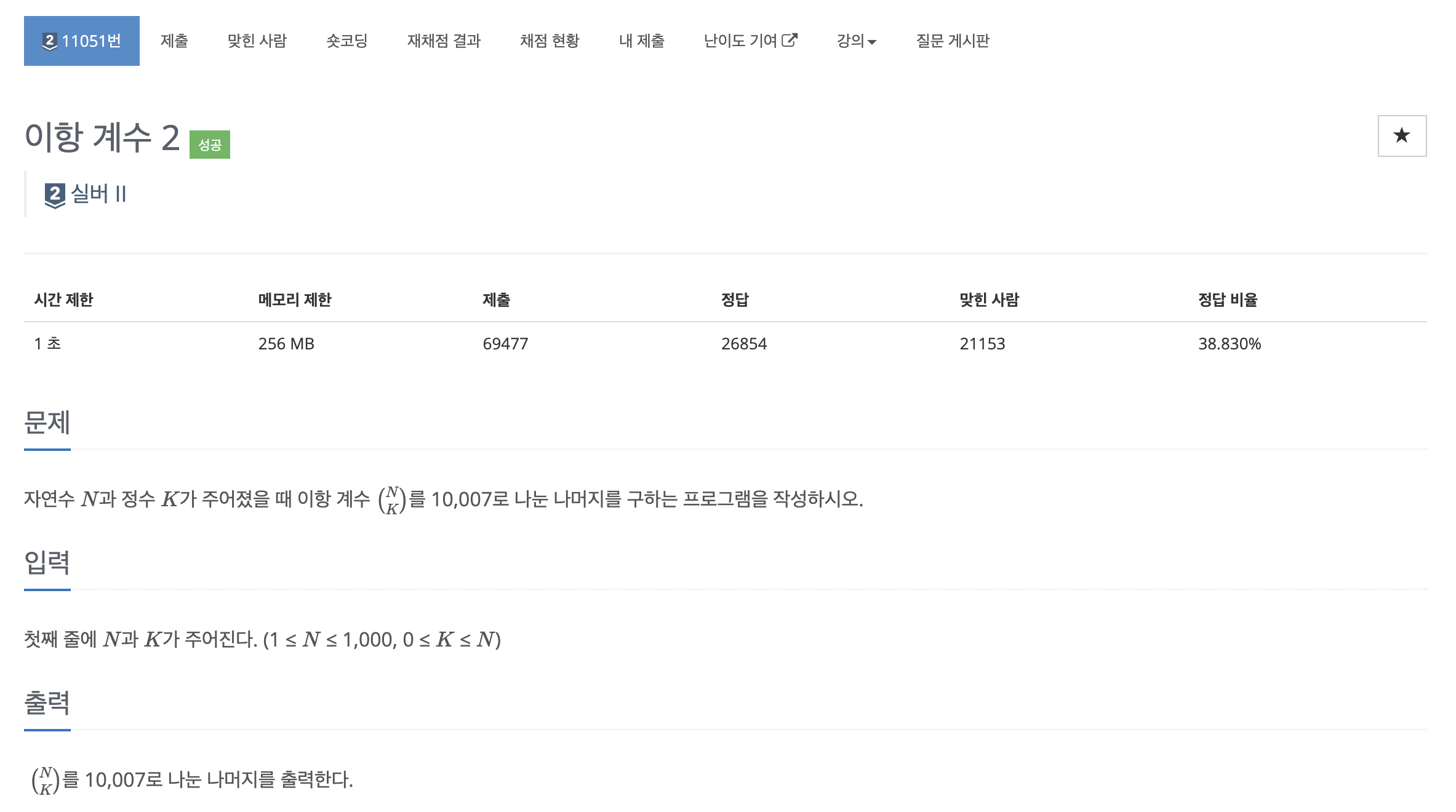
백준 11050번 - 이항 계수 1 해당 문제에서 $N$ 과 $K$ 의 범위가 더 커졌고, 이항 계수를 10,007로 나눈 나머지를 구해야 하는 문제다. 이항 계수는 팩토리얼 연산 때문에 수가 기하급수적으로 커지며 연산량도 많아져서 다이나믹 프로그래밍을 활용해서 효율적으로 구해야 한다.

또한 계산 중간에 기본 타입의 범위를 넘어갈 수 있는데, (a + b) mod M -> ((a mod M) + (b mod M)) mod M이 가능함을 활용해 미리 모듈러 연산으로 수를 작게 유지해줘야 한다.

---

코드

1. Top-Down dp [Java]

import java.io.*;
import java.util.*;

public class Main {

    private static final int MOD = 10_007;
    private static int[][] dp;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int K = Integer.parseInt(st.nextToken());

        dp = new int[1 + N][1 + K];

        System.out.println(nCr(N, K));
    }

    private static int nCr(int n, int r) {
        if (r == 0 || n == r) return 1;
        if (r == 1) return n;

        if (dp[n - 1][r] == 0) {
            dp[n - 1][r] = nCr(n - 1, r);
        }

        if (dp[n - 1][r - 1] == 0) {
            dp[n - 1][r - 1] = nCr(n - 1, r - 1);
        }

        return dp[n][r] = (dp[n - 1][r] + dp[n - 1][r - 1]) % MOD;
    }
}

2. Bottom-Up dp [Java]

import java.io.*;
import java.util.*;

public class Main {

    private static final int MOD = 10_007;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int K = Integer.parseInt(st.nextToken());

        int[][] dp = new int[1 + N][1 + K];
        for (int n = 0; n <= N; n++) {
            dp[n][0] = 1;

            for (int r = 1; r <= Math.min(n, K); r++) {
                dp[n][r] = (dp[n - 1][r] + dp[n - 1][r - 1]) % MOD;
            }
        }

        System.out.println(dp[N][K]);
    }
}

---

풀이 정보

1. Top-Down dp [Java]

• 7 min

2. Bottom-Up dp [Java]

• 2 min

---